【初中数学笔记】因式分解：从入门到入土

发表于 2025-08-18 更新于 2025-08-19 分类于初等数学本文字数： 4.2k 阅读时长 ≈ 15 分钟

因式分解指的是把一个整式分解成多个整式的乘积的过程。在因式分解中，通常要求各个因式的乘积都是既约多项式，即在规定数集内无法继续因式分解。

在初中数学中，因式分解作为数学学习的重点之一，其考察形式灵活多变，有诸多技巧。从提取公因式到待定系数法属于基础技巧，轮换对称式到既约多项式属于高级技巧。

提取公因式

提取公因式是因式分解中最基础技巧，几个整式都含有的因式称为它们的公因式。 \[ ma_1+ma_2+...+ma_n=m(a_1+a_2+...+a_n) \] 在提取公因式时，要注意一次提净。如果某个整式本身就是公因式，则需注意不要漏 \(1\).

例 1：因式分解：\(8a^3x^2-6ab^2xy^2-10ab^3xy\).

解：原式 \(=2ax(4a^2x-3b^2y^2-5b^3y).\)

公式法

在因式分解的时候有诸多公式可以使用，以下列出常见的公式，需牢记于心：

平方差公式：\(a^2-b^2=(a+b)(a-b)\)

立方差公式：\(a^3-b^3=(a-b)(a^2+ab+b^2)\)

上述公式的推广：\(a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+...+ab^{n-2}+b^{n-1})\)，\(n\) 为正整数且 \(n \geq 2\).
立方和公式：\(a^3+b^3=(a+b)(a^2-ab+b^2)\)

上述公式的推广：\(a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+...+a^2b^{n-3}-ab^{n-2}+b^{n-1})\)，\(n\) 为奇数且 \(n\geq 3\).
三项立方和公式：\(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)\)

推论：当 \(a+b+c=0\) 时，\(a^3+b^3+c^3 = 3abc\)
完全平方公式：\(a^2+2ab+b^2=(a+b)^2\)，\(a^2-2ab+b^2=(a-b)^2\)
三项完全平方公式：\(a^2+b^2+c^2+2ab+2bc+2ac=(a+b+c)^2\)
完全立方公式：\(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)，\(a^3-3a^2b+3ab^2-b^3=(a-b)^3\)

上述公式的推广：\((a+b)^n=a^n+C^1_na^{n-1}b+...+C^{n-1}_nab^{n-1}+b^n\)，\(n\) 为正整数且 \(n \geq 2\).

例 2：因式分解：\(a^6-b^6\).

解：原式 \(=(a^3-b^3)(a^3+b^3)\)

\(=(a+b)(a-b)(a^2-ab+b^2)(a^2+ab+b^2)\)

本题先利用了平方差公式，再利用了立方和公式与立方差公式，也可以先利用立方差公式。

十字相乘法

十字相乘法是指将整式 \(ax^2+bx+c\) 分解为 \((mx+n)(px+q)\)，其中 \(a=mp,bnp+mq,c=nq\).

如 \(6x^2+19x+15=(3x+5)(2x+3)\)，\(2x^2-5x-3=(2x+1)(x-3)\).

连续运用 \(2\) 次十字相乘法的方法称为双十字相乘法，其方法为 \[ ax^2+by^2+cxy+dx+ey+f=(mx+ny+s)(px+qy+t) \] 其中 \(a=mp\)，\(b=nq\)，\(c=mp+nq\)，\(d=mt+sp\)，\(e=nt+sq\)，\(f=st\).

在使用十字相乘法时,我们通常采用以下方法进行检验：

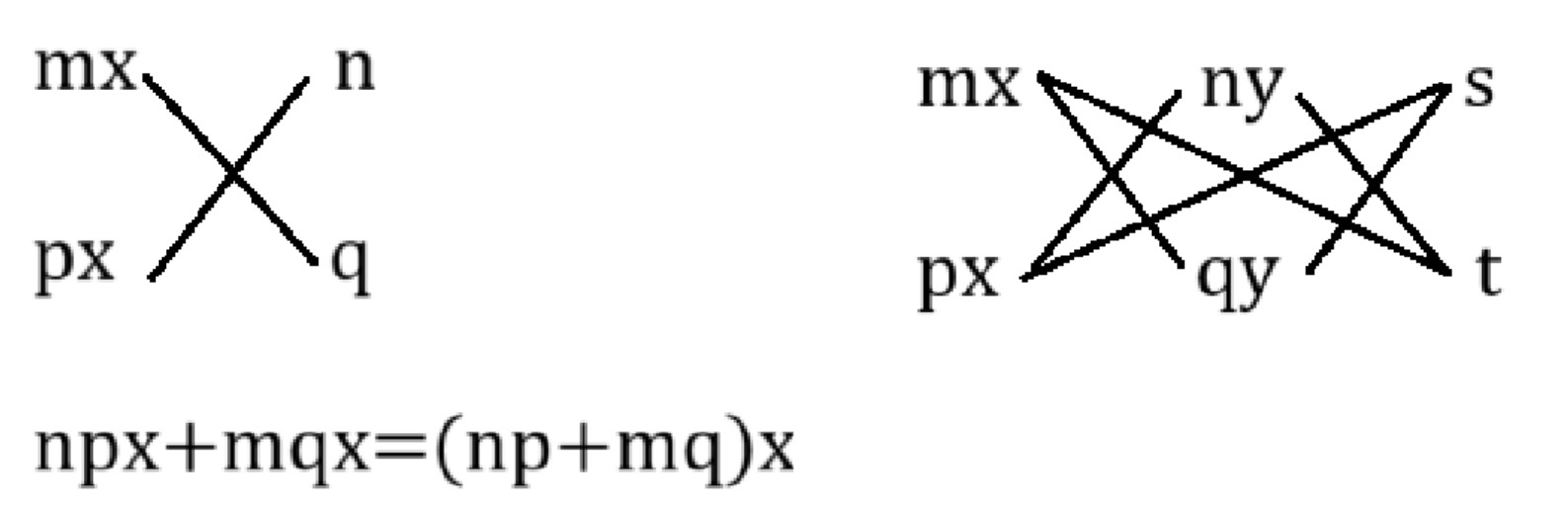
例 3：因式分解：\(2x^2-3xy-2y^2-xz+7yz-3z^2\).

解：原式 \(=(2x+y-3z)(x-2y+z)\)

分组分解法

分组分解法是一种常用的因式分解方法，主要思想是将多项式的各项按照一定规律进行分组，使得每一组中都能提取出一个公因式，然后再把这些公因式作为整体提取，进而完成因式分解。

常见的分组方式有两类：

直接分组：将多项式按顺序分成若干组，每一组提取公因式后，得到的结果中含有相同的括号因式。
巧妙分组：当直接分组无法出现公因式时，可以通过适当调整项的顺序或拆分、合并项，制造出相同的因式。

例 4：因式分解：\(ax-by-bx+ay\)

解：原式 \(=(ax-bx)+(ay-by)\)

\(=(a-b)x+(a-b)y\)

\(=(a-b)(x+y)\)

例 5：因式分解：\(x^2yz+axyz+yz-xy^2-xz^2-az^2\)

解：原式 \(=(axyz-az^2)+(x^2yz-xz^2)+(yz-xy^2)\)

\(=az(xy-z)+xz(xy-z)+y(z-xy)\)

\(=(az+xz-y)(xy-z)\)

分组分解法的关键在于分组的技巧，有时需要通过观察项之间的关系，灵活地调整顺序或分配方式，才能成功提取出公因式。

拆项与添项

拆项法：当原式不能直接分组时，可以把某一项“拆开”，让式子便于分组。
添项法：当多项式中缺少“关键项”时，可以巧妙地添加并同时减去同一个项，使式子便于分组。添项法的核心是“加减同一个量”，制造出某种常见公式结构（如完全平方、立方和差等）。

例 6：因式分解：\(a^3+b^3+3a^2+3b^2+3a+3b+2\)

解：原式 \(=(a^3+3a^2+3a+1)+(b^3+3b^2+3b+1)\)

\(=(a+1)^3+(b+1)^3\)

\(=(a+1+b+1)[(a+1)^2-(a+1)(b+1)+(b+1)^2]\)

\(=(a+b+2)(a^2+b^2-ab+a+b+1)\)

例 7：因式分解：\((1+y)^2-2x^2(1+y^2)+x^4(1-y)^2\)

解：原式

\(=[(1+y)^2+2(1+y)x^2(1-y)+x^4(1-y)^2]-2(1+y)x^2(1-y)-2x^2(1+y^2)\)

\(=[(1+y)+x^2(1-y)]^2-2x^2[(1-y^2)+(1+y^2)]\)

\(=(x^2-x^2y+y+1)^2-4x^2\)

\(=(x^2-x^2y+y+1+2x)(x^2-x^2y+y+1-2x)\)

\(=[(x+1)^2-y(x+1)(x-1)][(x-1)^2-y(x+1)(x-1)]\)

\(=(x+1)(x-1)[(x+1)-y(x-1)][(x-1)-y(x+1)]\)

\(=(x+1)(x-1)(x-xy+y+1)(x-xy-y-1)\)

主元法与换元法

主元法：在多元多项式中选定一个变量或一个常见整体作“主元”，把原式看成关于这个主元的一元多项式，其余字母视为常数；按一元多项式的常规方法（提公因式、公式法、十字相乘等）分解。
换元法：当多项式结构比较复杂时，可以通过“设元”的方式，用一个新字母代替复杂的部分，使表达式简化，然后分解，最后再代回。

例 8：因式分解：\(2x^3-x^2z-4x^2y+2xyz+2xy^2-y^2z\)

解：以 \(y\) 为主元降幂排列

原式 \(=(2x-z)y^2-2xy(2x-z)+x^2(2x-z)\)

\(=(2x-z)(x^2-2xy+y^2)\)

\(=(2x-z)(x-y)^2\)

整式的一次因式

整式的带余除法

设 \(f(x)\) 为 \(n\) 次多项式，\(g(x)\) 为 \(m\) 次多项式（\(n,m\) 为整数且 \(n>m\)），则 \[ f(x)=g(x)q(x)+r(x) \] 其中 \(q(x)\) 为商式，\(r(x)\) 为余式。

余数定理

设 \(g(x)=x-a\)，则 \(f(x)=(x-a)q(x)+r\)

令 \(x=a\)，则 \(f(a)=r\)，即 \(f(x)\) 除以 \(x-a\) 的余数等于 \(f(a)\).

由余数定理可以推出，若 \(f(a)=0\)，则 \(x-a\) 是 \(f(x)\) 的一个因式。

例9：因式分解：\(6x^4 - 5x^3 - 28x^2 + 13x + 30\)

解：当 \(x=-1\) 时，原式 \(=0\)，所以 \(x+1\) 是它的一个因式

原式 \(=(x+1)(6x^3-11x^2-17x+30)\)

当 \(x=2\) 时，\(6x^3-11x^2-17x+30=0\)，所以 \(x-2\) 也是它的一个因式

\((x+1)(6x^3-11x^2-17x+30)\)

\(=(x+1)(x-2)(6x^2+x-15)\)

\(=(x+1)(x-2)(2x-3)(3x+5)\)

整系数多项式的有理根

对于整系数多项式 \(f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)，设有理数 \(\frac{p}{q}\)（\(p,q\) 为整数且 \(p,q\) 互质）为其根，则 \[ f(\frac{p}{q})=a_n(\frac{p}{q})^n+a_{n-1}(\frac{p}{q})^{n-1}+...+a_1(\frac{p}{q})+a_0=0 \] 去分母得 \[ a_np^n+a_{n-1}p^{n-1}q+...+a_1pq^{n-1}+a_0q^n=0 \] 左式应能被 \(p\) 整除，但 \(q\) 与 \(p\) 互质，则 \(a_0\) 能被 \(p\) 整除，同理 \(a_n\) 能被 \(q\) 整除。

因此，\(\frac{p}{q}\) 是 \(f(x)\) 的根的必要条件为 \(p\) 是 \(a_0\) 的因数，\(q\) 是 \(a_n\) 的因数。

注意：\(p\) 是 \(a_0\) 的因数，\(q\) 是 \(a_n\) 的因数并不是 \(\frac{p}{q}\) 是 \(f(x)\) 的根的充分条件。

判别法

设 \(p\) 是 \(a_0\) 的因数，\(q\) 是 \(a_n\) 的因数，\(p,q\) 互质。若 \(p-q\) 不是 \(f(1)\) 的因数，则 \(x-\frac{p}{q}\) 不是 \(f(x)\) 的因式。

整式的二次因式

待定系数法

对于整系数的四次多项式，如果它没有有理系数的一次因式，则考虑它能否分解为两个二次因式的乘积。处理这种问题常用待定系数法。

例 10：因式分解：\(x^4+x^3+2x^2-x+3\)

解：运用待定系数法，设原式 \(=(x^2+ax+b)(x^2+cx+d)\)

因此 \[ \begin{cases} a+c=1 \\ b+d+ac=2 \\ bc+ad=-1\\ bd=3 \end{cases} \] 由于 \(b,d\) 为整数，则有 \(\begin{cases}b=1\\d=3\end{cases}\) 或 \(\begin{cases}b=-1\\d=-3\end{cases}\)，分别代入可解得整数解 \(\begin{cases}a=-1\\b=1\\c=2\\d=3\end{cases}\)，因此有

原式 \(=(x^2-x+1)(x^2+2x+3)\)

轮换式与对称式

如果多项式中任意两个字母互换后，多项式保持不变，则多项式为对称式。如果多项式中所有字母依次轮换后，多项式保持不变，则多项式为轮换式。对称式必定为轮换式，但轮换式不一定为对称式。

如果轮换式中含有某些字母的式子，则其必定含有所有同种形式但字母不同的式子。

例 11：分解因式：\(a^3(b-c)+b^3(c-a)+c^3(a-b)\)

解：将 \(a=b\) 代入，原式 \(=0\)，因此 \(a-b\) 是原式的一个因式，同理 \(b-c\)，\(c-a\) 也是原式的因式。由于原式是四次式，则应还有一个一次齐次轮换式。

设原式 \(=k(a-b)(b-c)(c-a)(a+b+c)\)，比较系数可得 \(k=-1\)，于是

原式 \(=-(a-b)(b-c)(c-a)(a+b+c)\)

可以看出，有时我们需要补充齐次轮换式：

一次齐次轮换式：\(k(a+b+c)\)
二次齐次轮换式：\(l(x^2+y^2+z^2)+m(xz+yz+xz)\)
三次齐次轮换式：\(l(x^3+y^3+z^3)+m(x^2y+y^2z+z^2x)+n(xy^2+yz^2+zx^2)+kxyz\)

例 12：分解因式：

\((y^2-z^2)(1+xy)(1+xz)+(z^2-x^2)(1+yz)(1+xy)+(x^2-y^2)(1+zx)(1+zy)\)

解：容易看出原式为轮换式，有因式 \((x-y)(y-z)(z-x)\).

将原式拆分为 \(xyz[x(y^2-z^2)+y(z^2-x^2)+z(x^2-y^2)]\)

\(+x(y+z)(y^2-z^2)+y(x+z)(z^2-x^2)+z(x+y)(x^2-y^2)\)

则可转换为齐次式处理，分别有：

\(xyz[x(y^2-z^2)+y(z^2-x^2)+z(x^2-y^2)]\)

\(=xyz(x-y)(y-z)(z-x)\)

\(x(y+z)(y^2-z^2)+y(x+z)(z^2-x^2)+z(x+y)(x^2-y^2)\)

\(=(x-y)(y-z)(z-x)(x+y+z)\)

两式相加即有原式 \(=(x-y)(y-z)(z-x)(x+y+z+xyz)\)

轮换式与对称式的分解，通常先导出一些一次因式，然后根据轮换式和对称式的特点，导出更多因式，最后其余的因式用待定系数法得出。

如果轮换式不是齐次式，则按照次数分为几个齐次轮换式的和，分解后再相加。

实数集与复数集的分解

二次三项式的分解

对于二次三项式 \(ax^2+bx+c (a \neq 0)\)，其在复数集的分解方法为： \[ ax^2+bx+c=a(x-x_1)(x-x_2) \] 其中 \(x_1,x_2\) 是方程 \(ax^2+bx+c=0\) 的两根。若 \(\Delta < 0\)，则方程无实数根，也就是说该二次三项式是在实数范围内的既约多项式。

如果将分解范围扩展到复数集，则引入虚数单位 \(i\) 的概念，\(i^2=-1\)，容易看出二次三项式在复数范围内一定可以分解，如 \(x^2+x+1\)，其在实数范围内无法分解，但在复数范围内有

原式 \(=(x-\frac{-1-3i}{2})(x-\frac{-1+3i}{2})=\frac{1}{4}(2x+1+3i)(2x+1-3i)\)

代数基本定理

代数基本定理：在复数集内，每个关于 \(x\) 的多项式至少有一个根。即对于多项式 \(f(x)=\displaystyle\sum_{i=0}^na_ix^i\)（\(n\) 为正整数），一定有复数 \(c\) 使得 \(f(c)=0\).

也就是说，在复数集内，只有一次多项式是既约多项式。\(n\) 次多项式在复数集内恰好有 \(n\) 个根，可以分解为 \(f(x)=a_n(x-x_1)(x-x_2)...(x-x_n)\).

由于实系数多项式的虚数根是两两共轭的，则我们把共轭的两项因式相乘： \[ [x-(a+bi)][x-(a-bi)]=x^2-2ax+(a^2+b^2) \] 为实系数多项式。

因此我们把所有共轭的因式相乘，即可得到 \(f(x)\) 在实数集内的分解。所以在实数集中既约多项式一定是一次因式或二次因式。

单位根

多项式 \(x^n-1\) 的根称为 \(n\) 次单位根，其复数集内有 \(n\) 个根，即 \(\sqrt[n]{1}\) 在复数集内有 \(n\) 个值。它们分别为 \[ \cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n} (k=1,2,...,n) \] 例 13：分解因式：\(x^3-1\)

解：在实数集内，\(x^3-1\) 只能分解为 \((x-1)(x^2+x+1)\).

运用单位根知识，原式 \(=(x-1)(x-\frac{-1+\sqrt{3}}{2})(x-\frac{-1-\sqrt{3}i}{2})\)

特别地，我们将三次虚单位根记作 \(\omega\)，如果 \(\omega\) 是实系数多项式的根，那么 \(x^2+x+1\) 就是 \(f(x)\) 的一个因式。

既约多项式

一个多项式 \(f(x)\) 若次数 \(\ge 1\)，并且在规定数集内不能分解为两个比它次数更低的多项式的乘积（除了单位元与它本身），那么 \(f(x)\) 就是既约多项式。

艾氏判别法

在有理数集内判断多项式是否为既约多项式，可以使用艾氏判别法：

设 \(f(x)\) 是一个整系数多项式，如果存在一个质数 \(p\) 满足以下条件：

\(p\) 不整除 \(a_n\).
\(p\) 整除其余的系数。
\(p^2\) 不整除 \(a_0\).

则 \(f(x)\) 在有理数集内是既约多项式。

艾氏判别法的证明较为复杂，可以参考《数学奥林匹克小丛书初中卷1：因式分解技巧》12.5。

例14：证明：\(x^2+x+1\) 在有理数集内为既约多项式。

证明：令 \(x=y+1\)，则原式 \(=(y+1)^2+(y+1)+1=y^2+3y+3\)

取 \(p=3\)，满足艾氏判别法，因此原多项式为既约多项式。

以 2 为模的算术

采用以 \(2\) 为模的算术，可以极大的减少整数与多项式的个数，使问题大为化简。如一次多项式只有 \(x\)、\(x+1\)，二次既约多项式只有 \(x^2+x+1\)。

例 15：证明：\(x^5+x^2-1\) 在有理数集内为既约多项式。

证明：如果原式不为既约多项式，则其一定有一次因式或二次因式。

采用以 \(2\) 为模的算术，可以知道原式一定能被 \(x\)、\(x+1\)、\(x^2+x+1\) 中的某一个整除，

则原式 \(=x^5-x^2+1=x^2(x^3-1)+1=x^2(x+1)(x^2+x+1)+1\)

因此，原式一定不被 \(x\)、\(x+1\)、\(x^2+x+1\) 中的某一个整除，则原式在有理数集内为既约多项式。

分圆多项式

在 \(n\) 次单位根中，如果 \(k\) 与 \(n\) 互质，则对应的单位根称为本原单位根。与 \(n\) 次本原单位根对应的一次因式之积为一个整系数多项式，被称为分圆多项式。如 \(x^{15}-1\) 的本原单位根对应的一次因式之积为： \[ x^8-x^7+x^5-x^4+x^3-x+1 \] 其为既约多项式得证明见《数学奥林匹克小丛书初中卷1：因式分解技巧》12.3

一般地，分圆多项式在有理数集内均为既约多项式。

绝对不可约

有些多元多项式在有理数集内不可约，但在扩大的数集内却可以分解，在复数集内不可约的多元多项式称为是绝对不可约的。如二元二次多项式 \(ax^2+bxy+cy^2+dx+ey+f\)，当 \[ 4acf+bed-cd^2-ae^2-fb^2 \neq 0 \] 时，该多项式是绝对不可约的。

如果上式等于 \(0\)，则该式在复数集内可以分解为两个一次因式之积。进一步地，如果 \(b^2-4ac \geq 0\)，\(d^2-4af \geq 0\)，\(e^2-4cf \geq 0\) 同时成立，则在实数集内就可以分解。更进一步地，如果三式都是有理数的平方，则上式可以在有理数范围内分解。