【高中数学笔记】不等式基础

发表于 2025-08-21 更新于 2025-08-30 分类于初等数学本文字数： 1.2k 阅读时长 ≈ 5 分钟

不等式是数学中表示两个数量之间大小关系的式子。它与方程类似，但用不等号来表示不相等的情况。不等式的解通常不是单个数，而是一个数集。

在高中数学里，我们将学习一元二次不等式、分式不等式、高词不等式、无理不等式、绝对值不等式、均值不等式和柯西不等式。

一元二次不等式

一元二次不等式的基本形式为 $ax^2+bx+c>0$ 或 $ax^2+bx+c \geq 0$ $(a>0)$. 我们通常与二次函数的图像结合在一起解一元二次不等式。

设方程 $ax^2+bx+c=0$ 的两根为 $x_1,x_2(x_1 \leq x_2)$，$\Delta=b^2-4ac$.

$\Delta >0$：$ax^2+bx+c>0$ 的解集为 $\{x|x<x_1或x>x_2\}$，$ax^2+bx+c < 0$ 的解集为 $\{x|x_1 < x < x_2 \}$.
$\Delta =0$：$ax^2+bx+c>0$ 的解集为 $\{x|x \neq -\frac{b}{2a}\}$，$ax^2+bx+c < 0$ 的解集为 $\varnothing$.
$\Delta < 0$：$ax^2+bx+c>0$ 的解集为 $\mathbb{R}$，$ax^2+bx+c < 0$ 的解集为 $\varnothing$.

分式不等式

分式不等式通常转换为整式不等式，同时考虑分母不能为零。

$\frac{f(x)}{g(x)}>0$：$f(x)g(x)>0$，在这种情况下，解集中一定不包含分母为 $0$ 的情况。
$\frac{f(x)}{g(x)} \geq 0$：$f(x)g(x)\geq 0$ 且 $g(x) \neq 0$.

高次不等式

高次不等式是指次数大于 $2$ 的多项式不等式，如 $x^3-4x^2+3>0$，通常将高次不等式整理为标准形式，然后将 $f(x)$ 因式分解，从而确定多项式的根。在数轴上画出 $f(x)$ 的粗略图像，通过图像判断不等式的解集，注意是否包含零点。具体口诀为 “奇穿偶不穿”，如果根的次数为奇数，则图像穿过零点，反之不穿过。

如 $x^3-4x^2+3>0$，因式分解为 $(x-1)(x^2-3x-3)>0$，三个根分别为 $x_1=1,x_2=\frac{3-\sqrt{21}}{2},x_3=\frac{3+\sqrt{21}}{2}$，画出图像：

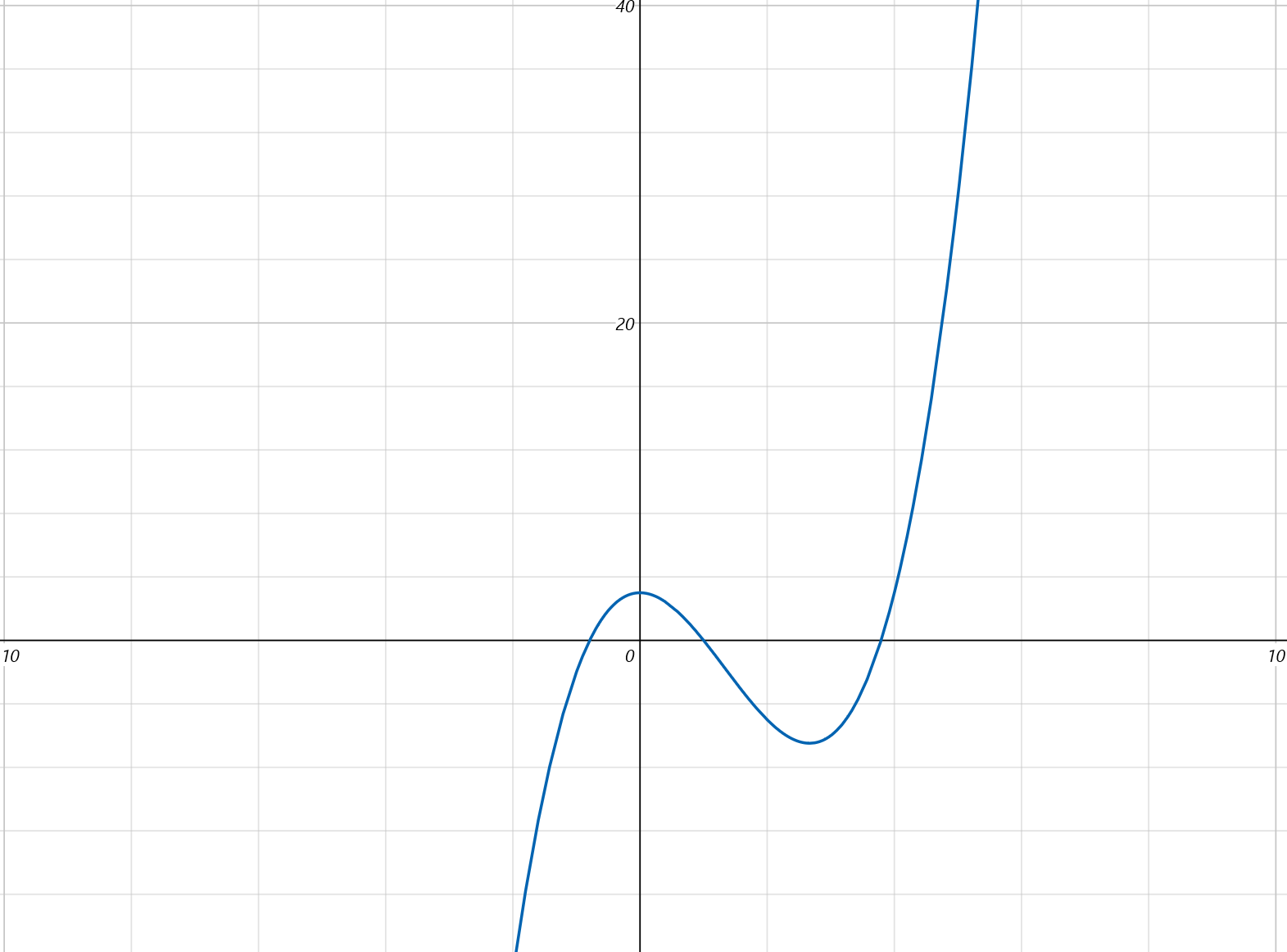
可以看出，原不等式的解集为 $(\frac{3-\sqrt{21}}{2},1) \cup (\frac{3+\sqrt{21}}{2},+\infty)$.

无理不等式

无理不等式指的是未知数含有根号的不等式，一般情况下我们将含有根号的部分放到一边，不含根号的部分放到另一边，然后两边平方。但同时要考虑根号内数的正负性。

$\sqrt{f(x)}>\sqrt{g(x)}$：$\begin{cases} f(x)\geq0\\g(x)\geq0\\f(x)>g(x)\end{cases}$
$\sqrt{f(x)}>g(x)$：$\begin{cases}f(x)\geq0\\g(x)\geq0\\f(x)>g(x)^2\end{cases}$ 或 $\begin{cases}f(x)\geq0\\g(x)<0\end{cases}$

绝对值不等式

绝对值不等式是指含有绝对值符号的、不等号连接的代数式。在解绝对值不等式时，要结合绝对值的定义，把它转化为普通不等式来求解。解绝对值不等式的方法通常有：1. 定义法；2. 零点分段法；3. 平方法；4. 图像法。其中零点分段法最为常用。

绝对值不等式中一个重要的不等式为三角不等式： \[ ||a|-|b|| \leq |a+b| \leq |a|+|b| \] 其中当 $a,b$ 同号时右边取等号，$a,b$ 异号时左边取等号。

基本不等式

由 $(a-b)^2 \geq 0$ 可知 $a^2-2ab+b^2 \geq 0$，即 $a^2+b^2 \geq 2ab$.

由 $(a-b)^2 \geq 0$ 可知 $(a+b)^2 \geq 4ab$，即 $ab \leq \frac{1}{4}(a+b)^2$.

$(a+b)^2 \geq 4ab$ 两边开平方得 $a+b \geq 2\sqrt{ab}$，当 $a=b$ 时取到等号。这个式子称为基本不等式。

基本不等式不仅适用于两个数，也可以推广到多个非负实数：

三个数：$\frac{a+b+c}{3}\geq \sqrt[3]{abc}$

$n$ 个数：$\frac{a_1+a_2+...+a_n}{n} \geq \sqrt[n]{a_1a_2...a_n}$，当 $a_1=a_2=...=a_n$ 时取到等号。

均值不等式

均值不等式是基本不等式的推广形式。记 $a_1,a_2,...,a_n$ 为 $n$ 个正实数，其一般形式为： \[ \sqrt{\frac{\sum a_i^2}{n}} \geq \frac{\sum a_i}{n} \geq \sqrt[n]{\prod x_i} \geq \frac{n}{\sum \frac{1}{x_i}} \] 当 $x_1=x_2=...=x_n$ 时取到等号。

为了方便记忆，我们称为平方平均 $\geq$ 算术平均 $\geq$ 几何平均 $\geq$ 调和平均。

柯西不等式

柯西不等式的二元形式：$(a_1^2+a_2^2)(b_1^2+b_2^2)\geq(a_1b_1+a_2b_2)^2$，当 $\frac{a_1}{b_1}=\frac{a_2}{b_2}$ 时取到等号。

柯西不等式的一般形式：$(\sum a_i^2)(\sum b_i^2)\geq(\sum a_ib_i)^2$.

柯西不等式的证明：

构造二次函数 $f(x)=(a_1x+b_1)^2+(a_2x+b_2)^2+...+(a_nx+b_n)^2$

$=(a_1^2+a_2^2+...+a_n^2)x^2+2(a_1b_1+a_2b_2+...+a_nb_n)x$

$+(b_1^2+b_2^2+...+b_n^2)$

由于 $f(x)\geq 0$ 恒成立，则由 $< 0 $ 可得 \[ 4(a_1b_1+a_2b_2+...+a_nb_n)^2-4(a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2)<0 \] 即 \[ (a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2)>(a_1b_1+a_2b_2+...+a_nb_n)^2 \]