【高中数学笔记】均值不等式的证明方法

​ 本文为 【高中数学笔记】不等式基础 的一个补充。

​ 设 \(a_1,a_2,...,a_n\) 是 \(n\) 个正实数，其平方平均 \(Q_n=\sqrt{\frac{a_1^2+a_2^2+...+a_n^2}{n}}\)，算术平均 \(A_n=\frac{a_1+a_2+...+a_n}{n}\)，几何平均 \(G_n=\sqrt[n]{a_1a_2...a_n}\)，调和平均 \(H_n=\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+...+\frac{1}{a_n}}\)。由均值不等式可知： \[ \min\{a_1,a_2,...,a_n\} \leq H_n \leq G_n \leq A_n \leq Q_n \leq \max\{a_1,a_2,...,a_n\} \] ​ 当且仅当 \(a_1=a_2=...a_n\) 时等号成立。

​ 均值不等式的证明方法有很多，数学归纳法、拉格朗日乘数法、琴生不等式法、排序不等式法、柯西不等式法等等，都可以证明均值不等式。

数学归纳法

​ 首先证明 \(A_n \geq G_n\)，先证 \(n=2^m(m\in \mathbb{R}^+)\) 时 \(A_n \geq G_n\) 成立。

​ 当 \(m=1\) 时，由基本不等式得 \(\frac{a_1+a_2}{2} \geq \sqrt{a_1a_2}\) 显然成立。

​ 假设当 \(m=k\) 时命题成立，则 \(m=k+1\) 时，

​ \(\sqrt[2^{k+1}]{a_1a_2...a_{2^k}...a_{2^{k+1}}}=\sqrt{\sqrt[2^k]{a_1a_2...a_{2^k}}\sqrt[2^k]{a_{2^k}a_{2^k+1}...a_{2^{k+1}}}}\)

​ \(\leq \frac{1}{2}(\sqrt[2^k]{a_1a_2...a_{2^k}}+\sqrt[2^k]{a_{2^k}a_{2^k+1}...a_{2^{k+1}}})\)

​ \(\leq \frac{1}{2}(\frac{a_1+a_2+...+a_{2^k}}{2^k}+\frac{a_{2^k+1}+a_{2^k+2}+...+a_{2^{k+1}}}{2^k})\)

​ \(=\frac{a_1+a_2+...a_{2^{k+1}}}{2^{k+1}}\)

​ 当且仅当 \(a_1=a_2=...=a_{2^{k+1}}\) 时取到等号。由数学归纳法可知 \(n=2^m(m\in \mathbb{R}^+)\) 时 \(A_n \geq G_n\) 成立。即 \(A_n \geq G_n\) 对无数个正整数 \(n\) 成立。

​ 假设 \(n=k+1\) 时命题成立，则当 \(n=k\) 时，令 \(b=\frac{a_1+a_2+...+a_k}{k}\)，有

​ \(\sqrt[k+1]{a_1a_2...a_kb} \leq \frac{a_1+a_2+...+a_k+b}{k+1}=\frac{kb+b}{k+1}=b\)，当且仅当 \(a_1=a_2=...=a_k\) 时取到等号。

​ 则 \(a_1a_2...a_kb \leq b^{k+1}\)，即 \(a_1a_2...a_k \leq b^k\).

​ 因此 \(\sqrt[k]{a_1a_2...a_k} \leq b = \frac{a_1+a_2+...+a_k}{k}\)，所以 \(n=k\) 时命题成立。由反向数学归纳法可知当正整数 \(n>1\) 时 \(A_n \geq G_n\) 成立。

​ 接下来证明 \(G_n \geq H_n\)，取 \(b_i=a_i\)，则由 \(A_n \geq G_n\)， \[ \frac{b_1+b_2+...+b_n}{n} \geq \sqrt[n]{b_1b_2...b_n} \] ​ 代入得 \[ \frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+...+\frac{1}{a_n}} \leq \sqrt[n]{a_1a_2...a_n} \] ​ 当且仅当 \(a_1=a_2=...=a_n\) 时等号成立。

​ 又因为 \(\displaystyle n\sum_{i=1}^n a_i^2-(\sum_{i=1}^na_i)^2=\sum_{i=1}^n a_i\sum_{j=1}^n(a_i-a_j)=\sum_{1 \leq i <j \leq n}(a_i-a_j)^2 \geq 0\)

​ 即 \(\displaystyle n\sum_{i=1}^n a_i^2 \geq (\sum_{i=1}^na_i)^2\) ，\(\sqrt{\frac{a_1^2+a_2^2+...+a_n^2}{n}} \geq \frac{a_1+a_2+...+a_n}{n}\)

​ 综上所述，\(Q_n \geq A_n \geq G_n \geq H_n\)，当且仅当 \(a_1=a_2=...=a_n\) 时取到等号。

二元形式的几何证明

​ 对于均值不等式的二元形式，我们可以通过几何法进行巧妙的证明。

​ 如图所示，\(CH \perp AB,AB \perp OG,CO \perp CM\).

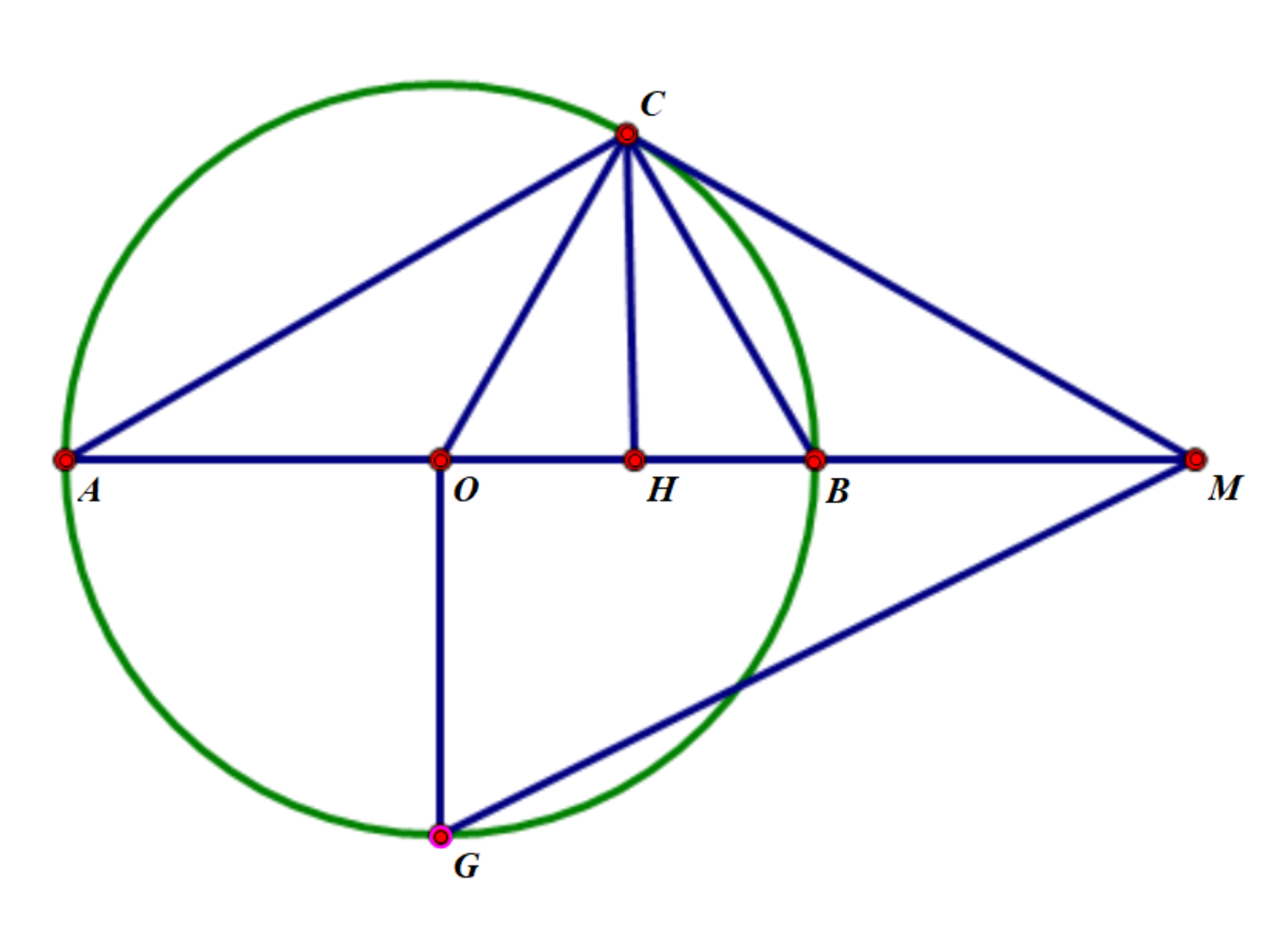
​ 设 \(AM=a,BM=b\)，不难发现，\(AO=CO=BO=\frac{a-b}{2}\),\(OM=\frac{a+b}{2}\),\(MC=\sqrt{AM·BM}=\sqrt{ab}\).

​ \(MG=\sqrt{OG^2+OM^2}=\sqrt{\frac{a^2+b^2}{2}}\),\(HM=\frac{MC^2}{OM}=\frac{ab}{\frac{a+b}{2}}=\frac{2}{\frac{1}{a}+\frac{1}{b}}\).

​ 在直角三角形中，\(MG>OM>CM>HM\)，即 \(\sqrt{\frac{a^2+b^2}{2}}>\frac{a+b}{2}>\sqrt{ab}>\frac{2}{\frac{1}{a}+\frac{1}{b}}\)