【高中数学笔记】两个重要极限的证明

发表于 2025-08-31 分类于初等数学本文字数： 727 阅读时长 ≈ 3 分钟

在高中内容中，有两个重要的极限：1. $\displaystyle\lim_{x \rightarrow 0}\frac{\sin x}{x}=1$；2. $\displaystyle \lim _{x \rightarrow \infty}(1+\frac{1}{x})^x = e$. 下面用夹逼定理证明这两个极限的存在性。

首先证明 $\displaystyle\lim_{x \rightarrow 0}\frac{\sin x}{x}=1$：

由于 $\displaystyle\frac{\sin x}{x}$ 是偶函数，所以证明 $\displaystyle\lim_{x \rightarrow 0^+}\frac{\sin x}{x}=1$ 即可，$\displaystyle\lim_{x \rightarrow 0^-}\frac{\sin x}{x}=1$ 同理。

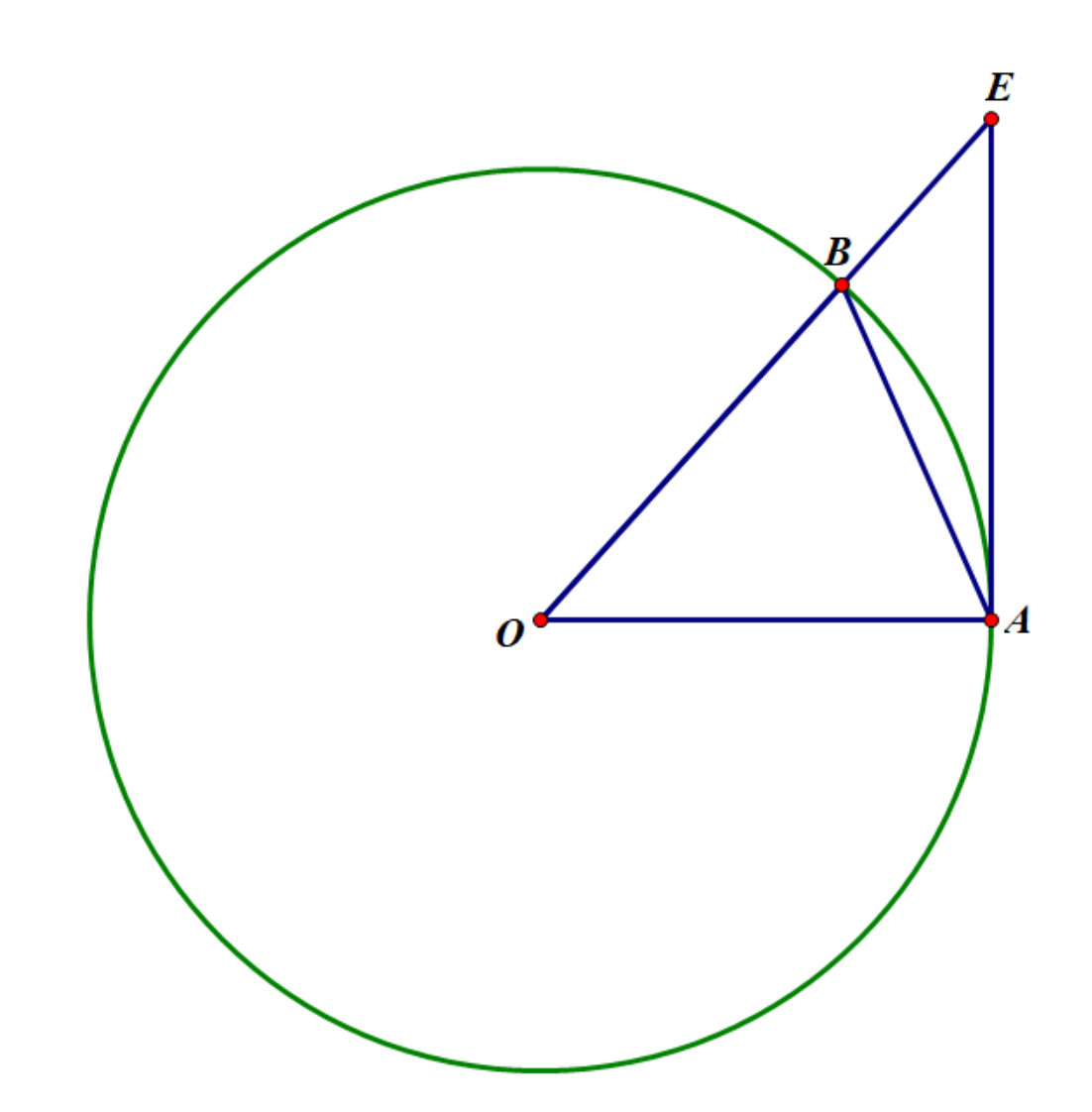
首先考虑 $0<x<\frac{\pi}{2}$ 的情况，在如图所示的单位圆中，$S_{\triangle ABO}<S_{扇形ABO}<S_{\triangle AOE}$，所以有 $\frac{1}{2}\sin x<\frac{1}{2}x<\frac{1}{2}\tan x$，即 $1<\frac{\sin x}{x}< \frac{1}{\cos x}$.

又有 $\displaystyle \lim_{x \rightarrow 0^+} \cos x=1$，即 $\displaystyle \lim _{x \rightarrow 0^+}\frac{1}{\cos x}=1$，根据夹逼定理即有 $\displaystyle \lim _{x \rightarrow 0^+}\frac{\sin x}{x}=1$.

当 $-\frac{\pi}{2}<x<0$ 时，令 $y=-x$，即 $0<y<\frac{\pi}{2}$，$x \rightarrow 0^- \Leftrightarrow y \rightarrow 0^+$，则 $\displaystyle \lim_{x \rightarrow 0 ^-}\frac{\sin x}{x}=\lim_{y \rightarrow 0 ^+}\frac{\sin x}{x} =1$，综上所述即有 $\displaystyle\lim_{x \rightarrow 0}\frac{\sin x}{x}=1$.

接下来证明 $\displaystyle \lim _{x \rightarrow \infty}(1+\frac{1}{x})^x = e$，该证明更加复杂。

首先证明数列 $(1+\frac{1}{n})^n$ 存在极限。令 $a_n=(1+\frac{1}{n})^n$，有：

$a_n=\displaystyle\sum_{i=0}^{n}C_n^i·(\frac{1}{n})^i=\sum_{i=0}^n\frac{1}{i!}·(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{i}{n})$，于是 $\displaystyle a_{n+1}=\sum_{i=0}^{n+1}\frac{1}{i!}·(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{i}{n})$.

做差可得 $a_{n+1}>a_n$，于是 $\{a_n\}$ 是一个单调递增序列。

又有 $a_n<\displaystyle\sum_{i=0}^{n}\frac{1}{i!}<1+1+\sum_{i=1}^{n-1} (\frac{1}{i}-\frac{1}{i+1})<3$，因此 $\{a_n\}$ 是一个单调有界数列，于是 $\displaystyle\lim_{n \rightarrow \infty}a_n$ 存在，其极限值是一个无理数，我们将其记作 $e$.

再证明 $\displaystyle\lim_{x \rightarrow \infty}(1+\frac{1}{x})^x=e$.

当 $x>0$ 时，令 $n=[x]$，于是 $\displaystyle 1+\frac{1}{n+1}<1+\frac{1}{x} \le 1 + \frac{1}{n}$，且 $\displaystyle (1+\frac{1}{n+1})^n\le (1+\frac{1}{x})^x \le (1+\frac{1}{n})^{n+1}$.

又 $\displaystyle \lim_{n\rightarrow +\infty}(1+\frac{1}{n+1})^{n}=\lim_{n\rightarrow +\infty}(1+\frac{1}{n+1})^{n+1-1}=\lim_{n\rightarrow +\infty}[(1+\frac{1}{n+1})^{n+1}·(1+\frac{1}{n+1})^{-1}]=e$.

$\displaystyle \lim_{n\rightarrow + \infty}\displaystyle (1+\frac{1}{n})^{n+1}=\lim_{n\rightarrow + \infty}[(1+\frac{1}{n})^n·(1+\frac{1}{n})]=e$.

另外 $x \rightarrow +\infty \Leftrightarrow n \rightarrow \infty$，由夹逼定理得 $\displaystyle\lim_{x\rightarrow+\infty}(1+\frac{1}{x})^x=e$.

当 $x<0$ 时，令 $y=-x$，$x-y +$，于是有

$\displaystyle(1+\frac{1}{x})^x=(1-\frac{1}{y})^{-y}=(1+\frac{1}{y-1})^y=(1+\frac{1}{y-1})^{y-1}·(1+\frac{1}{y-1})$.

因此 $\displaystyle\lim_{x \rightarrow -\infty}(1+\frac{1}{x})^x=\lim_{y\rightarrow +\infty}[(1+\frac{1}{y-1})^{y-1}·(1+\frac1{y-1})]=e$.

综上，有 $\displaystyle\lim_{x \rightarrow \infty}(1+\frac{1}{x})^x=e$.